回顾：矩阵乘法

二维矩阵乘法：

假设矩阵A是一个2行 x 3列的矩阵，矩阵B是一个3行 x 2列的矩阵，矩阵A乘以矩阵B得到结果矩阵C：

那么A x B就是矩阵A的第一行的3个元素分别与矩阵B第一列的3个元素分别相乘，然后求和，就得到矩阵C的第一行第一列的元素，其余元素以此类推：

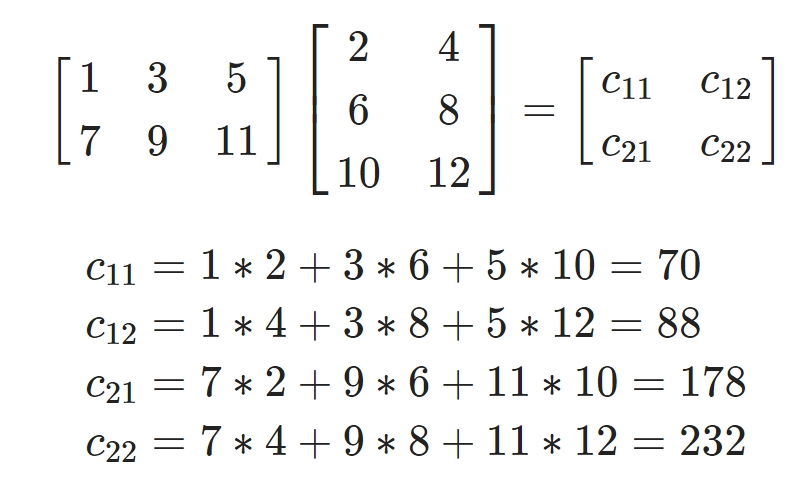
因此应该一个 m行 × n列 的矩阵，乘以一个 n行 × p列 的矩阵，那么 A * B 的结果将是一个 m行 × p列 的矩阵。

且计算矩阵A乘以矩阵B时，要求矩阵A的列数等于矩阵B的行数，否则无法计算。

矩阵乘法有以下特点：

• 不满足交换律
• 满足结合律

 

三位矩阵乘法：

假设有两个三维矩阵：

A = 
[[[ 1, 2, 3],
  [ 4., 5, 6]],
 [[ 7, 8, 9],
  [10, 11, 12]]]

B = 
[[[ 1, 2],
  [ 3, 4],
  [ 5, 6]],

 [[ 7, 8],
  [ 9, 10],
  [11, 12]]]

A矩阵如图所示：

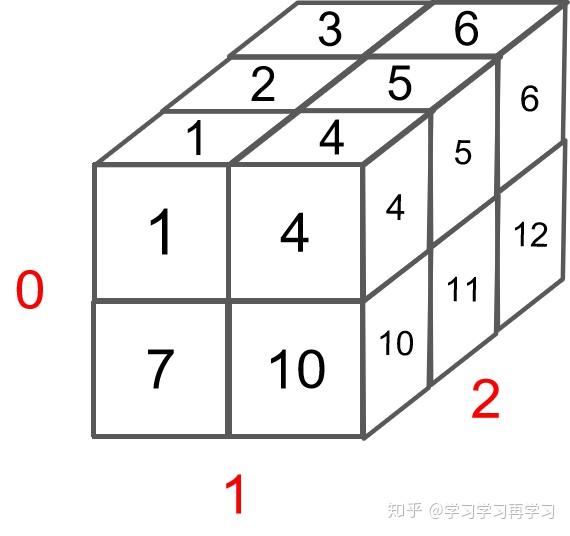
我们可以把3维矩阵看成是2个二维矩阵堆叠在一起：

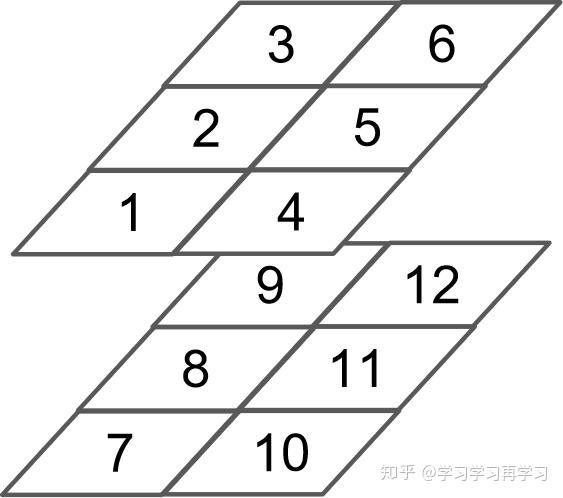
那么3维矩阵的乘法可以看成是2维矩阵相乘，然后将结果堆叠：

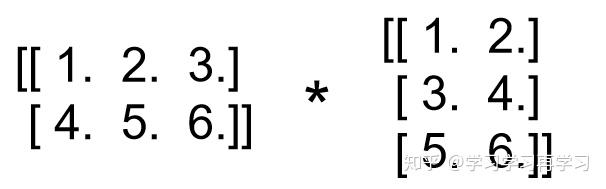
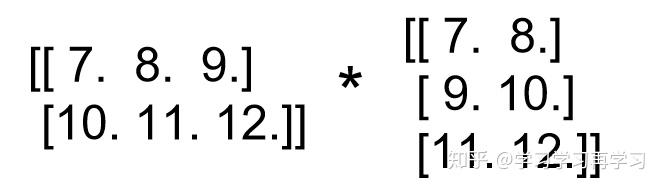
得到的结果为：

[[[ 22, 28],
  [ 49, 64]],

 [[220, 244],
  [301, 334]]]

 

参考链接：

https://zhaoyangchen.github.io/2023/07/03/matrix-multiply.html

https://zhuanlan.zhihu.com/p/337829793

 

关于线性代数部分的内容，推荐参阅麻省理工的开放课程-线性代数：

https://www.bilibili.com/video/BV1ix411f7Yp/